Das Thema dieses Artikels ist die Berechnung eines Polycarbonat-Baldachins mit Ihren eigenen Händen. Wir müssen lernen, die Hauptparameter der Struktur zu berechnen, die mit ihrer Stärke und ihren Abmessungen verbunden sind. So lass uns gehen.

Was berechnen wir
Wir müssen lernen zu rechnen:
- Die Dicke des Polycarbonats und die Tonhöhe der Kiste abhängig von der zu erwartenden Schneelast pro Quadratmeter.
- Abmessungen der Bogenabdeckung (was in Bezug auf die Geometrie auf die Berechnung der Bogenlänge hinausläuft).
Zur Verdeutlichung: Wir untersuchen Möglichkeiten, den Bogen für bekannten Radius und Winkel des Sektors zu berechnen, sowie für den Fall, dass wir nur die Abstände zwischen den Extrempunkten der Bogenoberfläche kennen.
- Minimaler Rohrquerschnitt mit bekannter Biegebelastung.
In dieser Reihenfolge gehen wir weiter.
Lattung und Schichtdicke
Beginnen wir mit der Berechnung der Schneelast.
Bevor wir herausfinden, wie ein Polycarbonat-Vordach berechnet wird, werden wir einige Annahmen formulieren, auf denen die Berechnung basiert.
- Die angegebenen Daten sind relevant für hochwertiges Material ohne Anzeichen einer Zerstörung durch UV-Strahlung. Polycarbonat ohne UV-Filter wird nach 2-3 Jahren Betrieb im Licht spröde.

- Wir vernachlässigen bewusst die begrenzte Verformungsstabilität der Kiste, die wir für absolut stabil halten.
Und jetzt - eine Tabelle, die Ihnen hilft, die optimale Dicke von Polycarbonat und den Abstand der Kiste zu wählen.
| Belastung, kg/m2 | Kistenzellenabmessungen mit Polycarbonatdicke, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050 x 790 | 1200 x 900 | 1320 x 920 | 1250 x 950 |
| 900 x 900 | 950 x 950 | 1000 x 1000 | 1100 x 1100 | |
| 820 x 1030 | 900 x 1100 | 900 x 1150 | 950 x 1200 | |
| 160 | 880 x 660 | 1000 x 750 | 1050 x 750 | 1150 x 900 |
| 760 x 760 | 830x830 | 830x830 | 970 x 970 | |
| 700 x 860 | 750 x 900 | 750 x 950 | 850 x 1050 | |
| 200 | 800 x 600 | 850 x 650 | 950 x 700 | 1100 x 850 |
| 690 x 690 | 760 x 760 | 780 x 780 | 880x880 | |
| 620 x 780 | 650 x 850 | 700 x 850 | 750 x 950 | |
Bogen
Berechnung nach Radius und Sektor
Wie berechnet man den Bogen für eine Überdachung, wenn man den Biegeradius und den Bogensektor kennt?

Die Formel sieht folgendermaßen aus: P=pi*r*n/180, wobei:
- P ist die Länge des Bogens (in unserem Fall die Länge einer Polycarbonatplatte oder eines Profilrohrs, das ein Element des Rahmens wird).
- pi ist die Zahl „pi“ (bei Berechnungen, die keine extrem hohe Genauigkeit erfordern, wird sie normalerweise mit 3,14 angenommen).
- r ist der Radius des Bogens.
- n ist der Bogenwinkel in Grad.
Lassen Sie uns als Beispiel mit unseren eigenen Händen die Länge des Überdachungsbogens mit einem Radius von 2 Metern und einem Sektor von 35 Grad berechnen.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 Meter.
Während des Arbeitsprozesses tritt häufig die gegenteilige Situation auf: Es ist notwendig, den Radius und den Sektor des Bogens an eine feste Länge des Bogens anzupassen. Die Gründe liegen auf der Hand: Der Preis von Polycarbonat ist hoch genug, um die Abfallmenge zu minimieren.
Offensichtlich ist in diesem Fall das Produkt des Sektors und des Radius gleich P/pi*180.
Versuchen wir, den Bogen unter eine 6 Meter lange Standardplatte zu passen. 6/3,14*180=343,9 (mit Rundung). Weiter - eine einfache Auswahl von Werten mit einem Taschenrechner in der Hand: Beispielsweise können Sie für einen Bogensektor von 180 Grad den Radius gleich 343,9 / 180 \u003d 1,91 Meter nehmen; Bei einem Radius von 2 Metern entspricht der Sektor 343,9 / 2 \u003d 171,95 Grad.
Berechnung nach Akkorden
Wie sieht die Berechnung des Designs einer Polycarbonat-Überdachung mit Bogen aus, wenn wir nur Informationen über den Abstand zwischen den Rändern des Bogens und seine Höhe haben?
Dabei kommt die sogenannte Huygens-Formel zur Anwendung. Um es zu verwenden, teilen wir die Sehne, die die Enden des Bogens verbindet, in zwei Hälften und zeichnen dann eine Senkrechte zur Sehne in der Mitte.
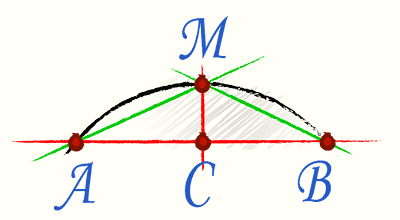
Die Formel selbst hat die Form Р=2l+1/3*(2l-L), wobei l der AM-Akkord und L der AB-Akkord ist.
Wichtig: Die Berechnung ergibt ein ungefähres Ergebnis. Der maximale Fehler beträgt 0,5 %; je kleiner der Winkelsektor des Bogens, desto kleiner der Fehler.
Berechnen wir die Länge des Bogens für den Fall, wenn AB \u003d 2 m und AM - 1,2 m sind.
P=2*1,2+1/3*(2*1,2-2)=2,4+1/3*0,4=2,533 Meter.
Berechnung des Schnittes mit bekannter Biegebelastung
Eine ziemliche Lebenssituation: Teil des Baldachins ist ein Visier von bekannter Länge. Wir können die Spitzenschneelast darauf ungefähr abschätzen. Wie wählt man ein Profilrohr mit einem solchen Querschnitt für Träger aus, damit es sich unter Last nicht verbiegt?

Beachten Sie! Wir gehen bewusst nicht darauf ein, wie die Belastung der Kappe berechnet wird. Die Beurteilung der Schnee- und Windlast ist ein völlig eigenständiges Thema für einen eigenen Artikel.
Zur Berechnung benötigen wir zwei Formeln:
- M = FL, wobei M das Biegemoment ist, F die auf das Ende des Hebels ausgeübte Kraft in Kilogramm ist (in unserem Fall das Gewicht des Schnees auf dem Visier) und L die Länge des Hebels ist (die Länge des Balkens, der die Last aus dem Schnee trägt, von der Kante bis zur Punktbefestigung) in Zentimetern.
- M/W=R, wobei W das Widerstandsmoment und R die Festigkeit des Materials ist.
Und wie wird uns dieser Haufen unbekannter Werte helfen?
An sich nichts. Für die Berechnung fehlen einige Bezugsdaten.
| Stahlsorte | Festigkeit (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Hinweis: Für professionelle Rohre werden normalerweise St3-, St4- und St5-Stähle verwendet.
Nun können wir anhand der uns vorliegenden Daten das Biegewiderstandsmoment des Profilrohrs berechnen. Lass uns das tun.
Angenommen, auf einer zwei Meter hohen Überdachung mit drei Tragbalken aus St3-Stahl lagern sich 400 Kilogramm Schnee an.Um die Berechnungen zu vereinfachen, einigen wir uns darauf, dass die gesamte Last auf den Rand des Visiers fällt. Offensichtlich beträgt die Last auf jedem Träger 400/3 = 133,3 kg; Bei einem zwei Meter langen Hebel beträgt das Biegemoment 133,3 * 200 \u003d 26660 kgf * cm.
Jetzt berechnen wir das Widerstandsmoment W. Aus der Gleichung 26660 kgf * cm / W = 2100 kgf / cm2 (Stärke des Stahls) folgt, dass das Widerstandsmoment mindestens 26660 kgf * cm / 2100 kgf / cm2 = 12,7 betragen sollte cm3.
Wie führt uns der Wert des Widerstandsmoments zu den Abmessungen des Rohrs? Durch die in GOST 8639-82 und GOST 8645-68 enthaltenen Sortimentstabellen, die die Abmessungen von quadratischen und geformten Rohren regeln. Sie geben für jede Größe das entsprechende Widerstandsmoment und für einen rechteckigen Abschnitt entlang jeder der Achsen an.
Nach Überprüfung der Tabellen stellen wir fest, dass die Mindestgröße eines Vierkantrohrs mit den erforderlichen Eigenschaften 50 x 50 x 7,0 mm beträgt; rechteckig (mit vertikaler Ausrichtung der größeren Seite) - 70 x 30 x 5,0 mm.

Abschluss
Wir hoffen, den Leser nicht mit einer Fülle trockener Zahlen und Formeln überfordert zu haben. Weitere Informationen zu den Methoden zur Berechnung und Auslegung von Polycarbonat-Vordächern finden Sie wie immer im Video in diesem Artikel. Viel Glück!
Hat Ihnen der Artikel geholfen?